Pada Kelas 4 Sekolah Dasar semester 1 dengan standar Kompetensi Memahami dan menggunakan sifat-sifat operasi hitung bilangan dalam pemecahan masalah. Dengan Kompetensi Dasar Mengidentifikasi sifat-sifat operasi hitung,
Tujuan Pembelajaran Siswa dapat Mengetahui jenis operasi hitung dengan penanaman nilai disiplin ( Discipline ) (NK, disiplin ( Discipline )
- Siswa dapat Memberikan contoh sehari-hari yang berhubungan dengan operasi hitung
- Siswa dapat Melakukan penjumlahan dan perkalian dengan nol
- Siswa dapat Melakukan perkalian dengan satu
- Siswa dapat Melakukan perkalian dua angka dengan angka sebelas
- Siswa dapat Melakukan penjumlahan dan perkalian tiga bilangan berurutan
- Siswa dapat Mengidentifikasi sifat penyebaran dalam perhitungan secara tekun ( diligence ) ( NK. tekun ( diligence )
Operasi Hitung Bilangan
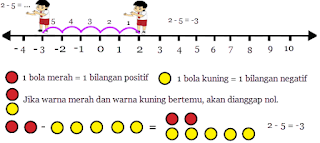
Penjumlahan dan pengurangan bilangan bulat , menjumlahkan bilangan positif, menjumlahkan bilangan bulat negatif menjumlahkan bilangan bulat postif dan negatif
Menjumlahkan bilangan bulat negatif dengan bilangan positif.
Contoh -6 + 8 = 2, digambarkan pada garis bilangan.
Perkalian Bilangan Bulat
Perkalian adalah penjumlahan berulang sebanyak bilangan yang dikalikan.
Contoh:
2 x 3 - 3 + 3 = 6
Sifat-sifat perkalian suatu bilangan
a. Perkalian bilangan positif dengan bilangan positif, hasilnya positif.
Contoh:
1) 4 x 5 = 5 + 5 + 5 + 5 = 20
2) 7 x 8 = 56
3) 12 x 15 = 180
b Perkalian bilangan positif dengan bilangan negatif, hasilnya negatif.
Contoh:
1) 4 x (-5) = (-5) + (-5) +(-5) +(-5) = -20
2) 7 x (-8) = -56
3) 12 x (-15) = -180
c. Perkalian bilangan negatif dengan bilangan positif, hasilnya negatif.
Contoh:
1) -4 x 5 = -(5 + 5 + 5 + 5) = -20.
2) -7 x 8 = -56
3) -12x 15 = -180
d. Perkalian bilangan negatif dengan bilangan negatif, hasilnya positif.
Contoh:
1) -4 x (-5) = -[-5 + (-5) + (-5) + (-5)] = -[-20] = 20
2) -7 x (-8) = 56
3) -12 x (-15) = 180
Kesimpulan :
1. + X + = +
2. + X - = -
3. - X + = -
4. - X - = +
Pembagian bilangan bulat
Pembagian merupakan operasi kebalikan dari perkalian
Contoh
12 : 4 = 3, karena 4 x 3 = 12 atau 3 x 4 = 12
42 : 7 = 6, karena 7 x 6 = 42 atau 6 x 7 = 42
Sifat-sifat pembagian bilangan bulat
a. Pembagian bilangan positif dengan bilangan positif, hasilnya positif
Contoh
1) 63 : 7 = 9
2) 143 : 11 = 13
b. Pembagian bilangan positif dengan bilangan negatif, hasilnya negatif
Contoh:
1) 63 : (-9) = -7
2) 72 : (-6) = -12
c. Pembagian bilangan negatif dengan bilangan positif, hasilnya negatif
Contoh:
1) -63 : 7 = -9
2) -120 : 10 = -12
d. Pembagian bilangan negatif dengan bilangan negatif, hasilnya positif.
Contoh:
1) -72 : (-8) = 9
2) -120 : (-12) = 10
Menggunakan Sifat Operasi Hitung Bilangan Bulat
Sifat komutatif
Sifat komutatif (pertukaran) pada penjumlahan dan perkalian.a + b = b + a
a x b = b x a, berlaku untuk semua bilangan bulat
Contoh:
1) 2 + 4 = 4 + 2 = 6
2) 3 + 5 = 5 + 3 = 8
3) 4 x 2 = 2 x 4 = 8
4) 3 x 2 = 2 x 3 = 6
Sifat asosiatif
Sifat asosiatif (pengelompokan) pada penjumlahan dan perkalian.(a + b) + c = a + (b+c)
(a x b) x c = a x (bxc), berlaku untuk semua bilangan bulat
Contoh:
1) (2+4) + 6 = 2 + (4+6) = 12
2) (3+6) + 7 = 3 + (6+7) = 16
3) (3x2) x 4 = 3 x (2x4) = 24
4) (3x5) x 2 = 3 x (5x2) = 30
Sifat distributif (penyebaran)
a x (b + c) = (a x b) + (a x c), yang berlaku untuk semua bilangan bulat.Contoh
1) 4 x (5 + 2) = (4 x 5) + (4 x 2) = 28
2) 5 x (7 + 3) = (5 x 7) + (5 x 3) = 50
Metode guru yang bisa digunakan sebagai berikut:
Metode Pembelajaran, Games, Tanya Jawab, dan Latihan dengan Alat/Bahan dan Sumber Belajar
Buku Pelajaran Matematika untuk Sekolah Dasar Kelas 4,
Buku lain yang relevan
Kegiatan keseharian yang relevan
Media Pembelajaran